Word Embeddings

Introducing Word Embeddings

• A word embedding is a vectorial representation of a word
• A word embedding is made up of trainable similarity values
• The length of a word embedding is the number of words in our vocabulary

• The number of word embeddings is an adjustable hyperparameter

  • It refers to the number of contextual traits we're interested in learning about our words
• In the following example, we only learn $3$ word embeddings:

• A word embedding can have any of the following interpretations:

  • It uncovers a semantic meaning of the words in our vocabulary
  • It approximates the similarity of certain words in our vocabulary
  • It represents a hidden semantic relationship

• For example, a word embedding may have similarly large values for:

  • Kitten and Cat
  • Pizza and Sandwich
  • House and home

• Specifically, a word embedding has the following properties:

  • It is a vector of (non-binary) numeric values
  • It has a size equal to the number of words in the vocabulary

Motivating Word Embeddings

• Machine learning algorithms require words to be in vector format
• So, we must find a way to convert free-text words into numeric values
• One of the simplest conversion techniques is one-hot encoding:

$$\text{Corpus} = [\text{banana}, \text{orange}, \text{yellow}]$$ $$\text{Vocab} = [\text{banana}, \text{orange}, \text{yellow}]$$ $$encode(\text{Vocab}) = \begin{bmatrix} 1 & 0 & 0 \\ 0 & 1 & 0 \\ 0 & 0 & 1 \end{bmatrix}$$

• The one-hot encoding method is inefficient for two related reasons:

  • The vectors become sparse
  • The number of dimensions grows very large
  • They lack any semantic meaning
• Instead, word embeddings can be learned

• Then, they can maintain the following traits:

  • They aren't sparse
  • The number of dimensions are adjustable
  • They carry some semantic meaning
• Then, a word embedding becomes an efficient representation of the words in a vocabulary
• The following is an example of $2$ word embeddings:

$$\text{Corpus} = [\text{banana}, \text{orange}, \text{yellow}]$$ $$\text{Vocab} = [\text{banana}, \text{orange}, \text{yellow}]$$ $$embed(\text{Vocab}) = \begin{bmatrix} 0.9 & 0.7 \\ 0.8 & 0.2 \\ 0.1 & 0.8 \end{bmatrix}$$

Describing Word Embeddings

• As stated already, the size of a word embedding equals the number of words in the vocabulary
• The number of word embeddings is an adjustable hyperparameter
• Adding additional word embeddings to a model will capture more context about the words
• However, adding additional word embeddings will slow down training
• Contextual information is useful for learning meaning and relationships of words
• This is because similar words typically appear in similar context

• In general, there are two approaches for learning word embedding:

  • Count-Based Models
  • Context-Based Models

Describing Count-Based Models

• These models rely on a co-occurrence (or word frequency) matrix
• It assumes that words in the same contexts share similar or related semantic meanings
• The model maps co-occurrences between neighboring words down to small and dense word vectors

• The following are examples of count-based models:

  • PCA
  • Topic models
  • Neural probabilistic language models

Describing Context-Based Models

• Context-based models predict a word given its neighbors
• The weights in the word vectors are model parameters
• As a result, the best vector representation of each word is learned during the model training process

Defining a Skip-Gram Context-Based Model

• There is a sliding window of fixed size moving along a sentence

  • Where, the word in the middle is the target
  • Where those words on its left and right within the sliding window are the context words
• The skip-gram model is trained to predict the probabilities of a word being a context word for a given target

• The following example includes observations with:

  • A target word
  • The associated context words as training samples
  • The associated 5-word sliding window along the sentence

The man who passes the sentence should swing the sword.

Sliding Window (n=5)	Target	Context
[the, man, who]	[the]	[man, who]
[the, man, who, passes]	[man]	[the, who, passes]
[the, man, who, passes, the]	[who]	[the, man, passes, the]
[man, who, passes, the, sentence]	[passes]	[the, man, the, sentence]
...	...	...
[sentence, should, swing, the, sword]	[swing]	[sentence, should, the, sword]
[should, swing, the, sword]	[the]	[should, swing, sword]
[swing, the, sword]	[sword]	[swing, the]

• Each context-target pair is treated as a new observation in the data

• For example, the target word swing produces four training samples:

  • (swing, sentence)
  • (swing, should)
  • (swing, the)
  • (swing, sword)

Architecture of Skip-Gram Context-Based Model

• We're given a vocabulary size V
• We learn word embedding vectors of size N
• The model learns to predict one context word (output)
• To do this, the model uses one target word (input) at a time

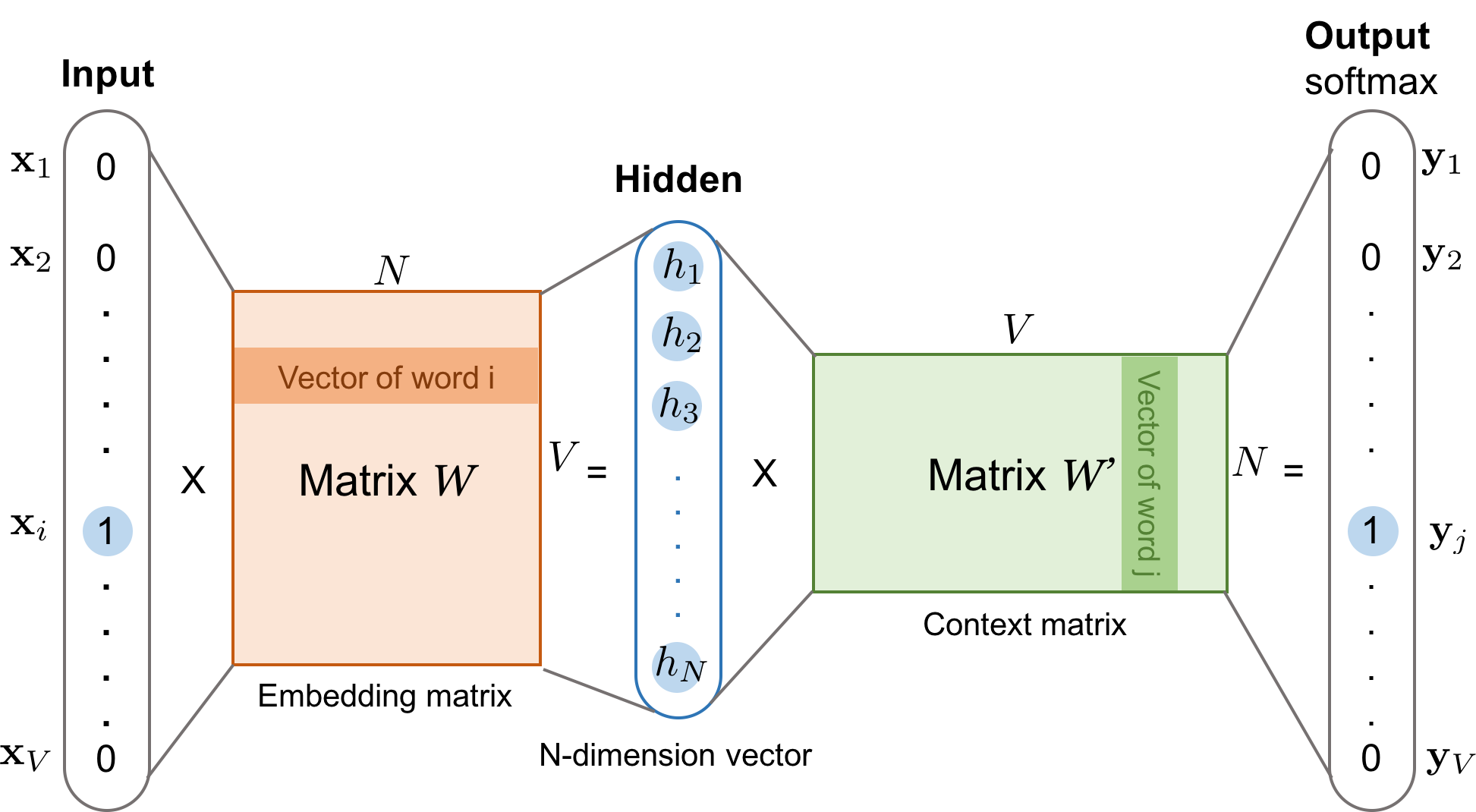
• Both input word $w_{i}$ and the output word $w_{j}$ are one-hot encoded into binary vectors $x_{i}$ and $y_{j}$ of size V
• Here, $W$ represents the word embedding matrix of size $V \times N$

• Multiplying $x_{i}$ and $W$ outputs the embedding vector of the input word $w_{i}$

  • Located in the $i^{th}$ row of $W$
  • The goal of this weight matrix is to squeeze the one-hot encoded vectors into a lower dimensional representation

• This newly discovered embedding vector forms the hidden layer

  • This embedding vector has $N$ dimensions

• Now, we have another word context matrix $W'$ of size $N \times V$

  • This matrix encodes the meanings of words as context
  • The goal of this weight matrix is to provide context to the word embeddings
• Multiplying the hidden layer and $W'$ outputs the one-hot encoded vector $y$
• Note, the $W$ and $W'$ try to achieve different things

Defining a Continuous Bag-of-Words Context-Based Model

• The Continuous Bag-of-Words (CBOW) also learns word vectors
• Recall, the skip-gram model predicts context words given a target
• Inversely, the CBOW model predicts a target word given context words

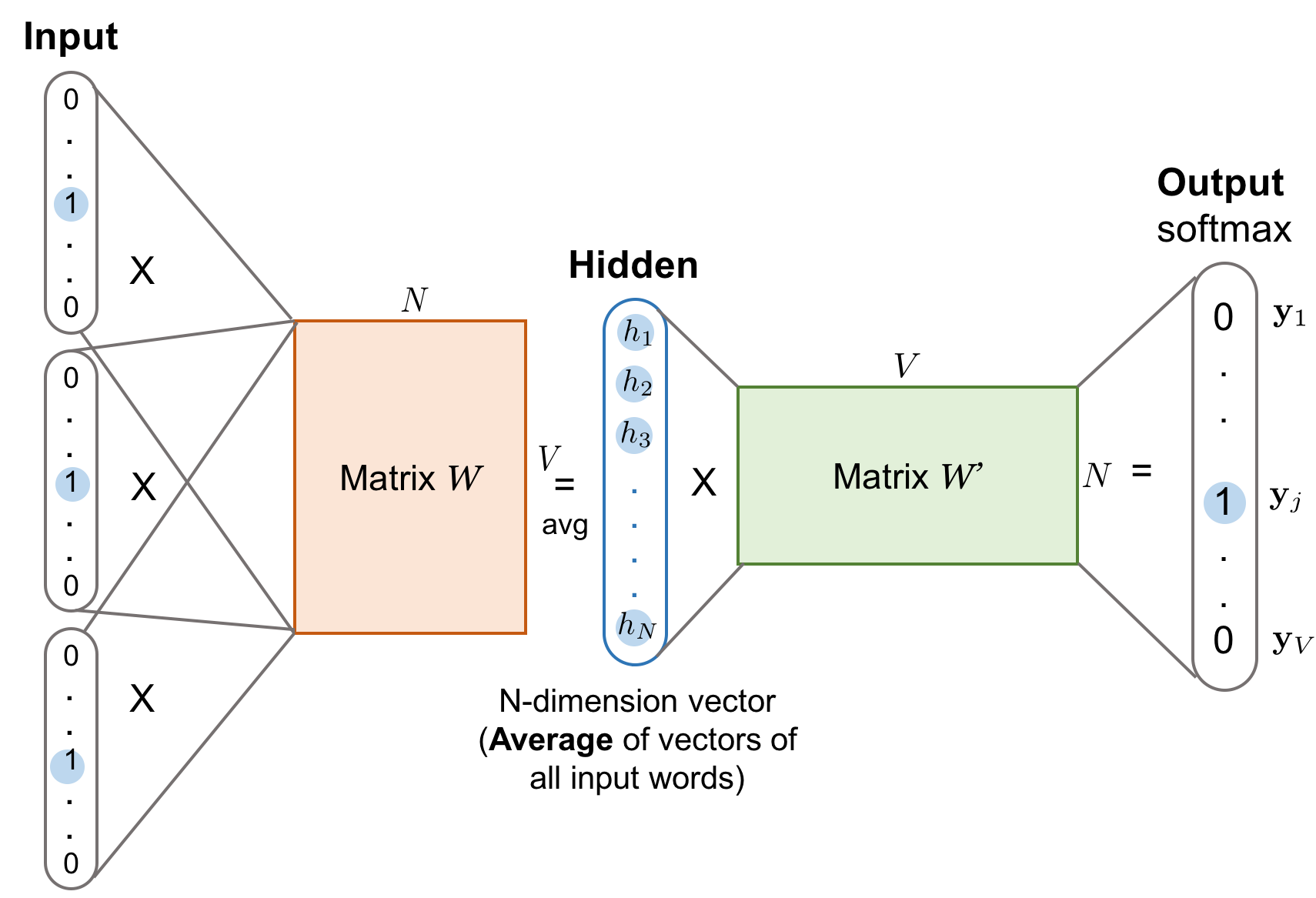
• Word vectors of multiple context words are averaged to get a fixed-length vector as in the hidden layer
• In other words, we average the word vectors, since there are multiple contextual words $w$
• Specifically, $w$ is the input vector and the matrix $W$ multiplied together
• Because the averaging stage smoothes over a lot of the distributional information, some people believe the CBOW model is can perform as well on a small dataset

References

• Learning Word Embedding Blog Post
• Paper about Word Representations in Vector Space
• Difference between Weight Matrices in Word2Vec