Sound Waves

How Sound Travels

In physics, many different forms of vibrations travel through various mediums around the world. For example, vibrations can travel through the air, water, or even a gas. These vibrations are represented using waves. In general, there are two basic types of waves:

• Mechanical Waves
• Electromagnetic Waves

Roughly, we can think of mechanical waves as sound waves and electromagnetic waves as light waves. There are exceptions to this generalization, which are illustrated in the graphic below.

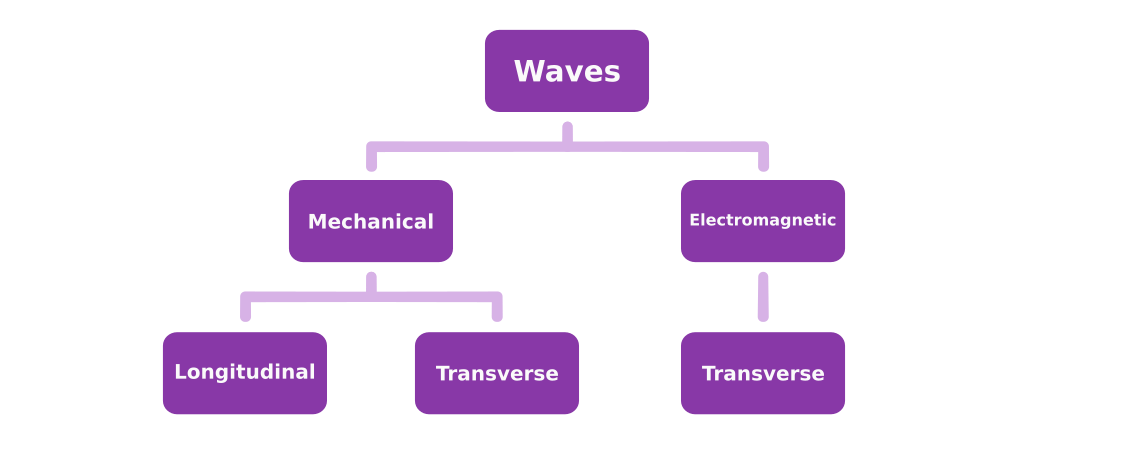
Sound waves refer to any vibration that is able to travel through a medium. On the other hand, light waves refer to any vibration that is able to travel through a vacuum. Meaning, they must be able to travel through a space without a medium.

There are many different types of sounds waves, which include audible and inaudible sound waves. Interestingly, there are only certain sound waves that are audible to humans. In particular, our ears can only hear waves having frequencies within the range of 20 Hz and 20,000 Hz. These sounds waves translate to waves with wavelengths between 0.67 inches and 56 feet.

To illustrate this point, a dog whistle is inaudible to the human ear. In other words, a dog whistle creates sound waves producing frequencies greater than 20,000 HZ, which fall outside of the hearing range for humans. However, they fall within the range of frequencies that are audible to dogs. In contrast, certain animals, such as whales and giraffes, communicate using sound waves that fall below 20 HZ sometimes. Meaning, some of their sound waves are audible to other whales and giraffes, but not humans. Avalanches and earthquakes also produce sound waves below the 20 HZ threshold.

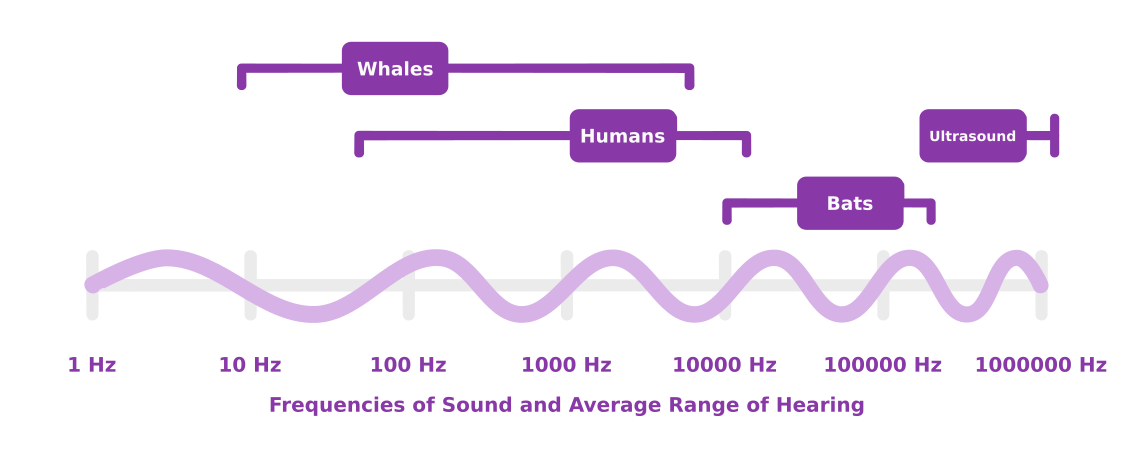
At this point, some of this information may seem convoluted. In the next section, we’ll develop a greater intuition for some of these technical terms, such as frequencies and wavelengths.

Science of Sound

Many different professions are interested in similar concepts related to sound. Specifically, musicians and engineers both use their own terminology for describing loudness and pitch. Engineers typically refer to any inherent change in a waveform, such as amplitude, whereas musicians refer to the acoustic effect caused by an increased amplitude. Moreover, waves with a higher frequency produce a higher-pitched sound, and waves with a higher amplitude produce a louder sound. They are both essentially talking about the same thing.

Returning to our dog whistle example, these sound waves produce an extremely high-pitched sound that is only audible to dogs. These sound waves are high-pitched because their frequencies are so high. On a related note, most dog whistles are fairly loud. These sound waves are loud because their amplitude is high.

There are two types of waves with their own distinct set of properties:

• Transverse Waves
• Longitudinal Waves

Transverse waves move in a single direction with some perpendicular oscillation. Most waves are transverse waves, including electromagnetic waves and water waves. These waves take the shape of a shoelace wiggling up and down.

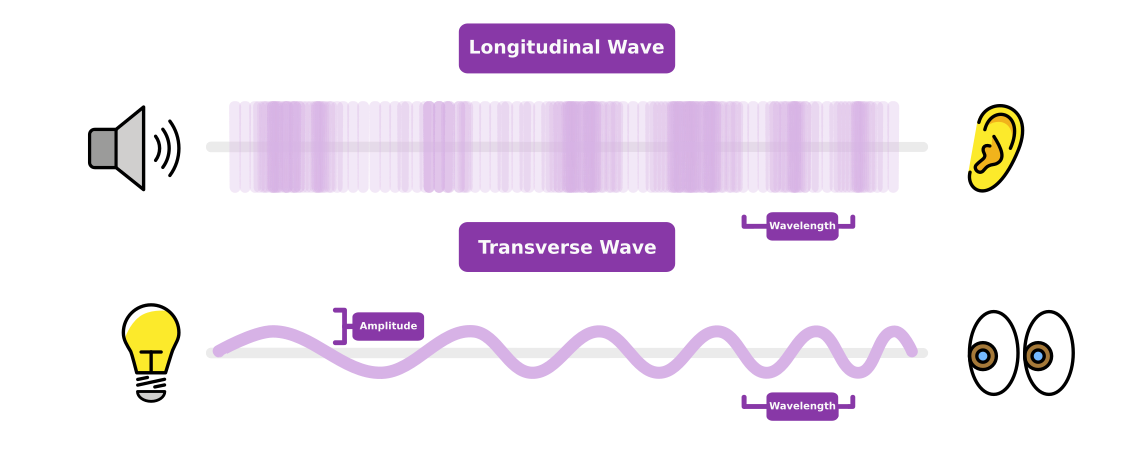
Longitudinal waves move in a single direction with parallel particle displacement. These waves take the shape of a slinky being pushed and pulled. There are only a few examples of longitudinal waves, which includes sound waves. The amplitude of a longitudinal wave measures a change in pressure. Although sound waves are longitudinal waves, most diagrams will represent sound waves as transverse waves, since this seems to be more intuitive for most people.

Sine Waveform

As stated previously, volume corresponds to the amplitude of pressure. Waves with larger amplitudes produce very loud sounds, which may even be felt by the body. In music, decibals are used to measure sounds, whereas frequency is measured in units of hertz. Note, decibels are a logarithmic ratio of the relative amplitude levels between two sounds.

In music theory, a sine wave is the most basic model of sound. Each sine wave has the following formula:

Here, $A$ refers to the amplitude of the wave. Mathematically, $\omega = \pi \times frequency$. Next, $t$ represents time. Lastly, $\varphi$ is an angle representing the number of periods.

A sine wave retains its general shape when combined with another sine wave of the same parameters, such as frequency, phase, and amplitude. It is the only periodic waveform that has this property. For this reason, the sine wave is acoustically unique. Sine waves are important in many areas of engineering and physics, since they maintain this property. In particular, sine waves are important in Fourier analysis, which roughly refers to the study of how a complex wave can be dissected into many simpler waves. In other words, Fourier analysis illustrates how any complex waveform may consist of a series of individual sine waves. Interestingly, there are plenty of use cases for Fourier analysis throughout many areas of engineering, including the design of hearing aids.

So far, we've defined a sine wave, specified its mathematical parameters, and introduced its importance in engineering. Now, let's illustrate some of these concepts by visualizing a sine wave as a transverse wave. A basic sine wave, where amplitude=60dB and frequency=262Hz, may look like the following:

We've all probably seen a sine wave that looks very similar to this before. Let's say this sine wave is the result of a note being played on a piano. In particular, a middle C may produce a sound wave appearing very similar to the sound wave illustrated above. The middle C key can be referred to as C4, and hitting the C4 key will produce a sound at 262 Hz, which has the same frequency as the sine wave above.

Now, what happens if we hit this piano key even harder? The sound will produce the same frequency as the sound before. However, the sound will be much louder, which means the amplitude increases. The amplitude of our previous sound wave was 60 dB, whereas the amplitude of our new sound wave becomes 70 dB. In the end, our new sound will correspond to a sine wave that could look like the following:

Notice, the crests and troughs stretch further away from the origin, compared to the crests and troughs of the previous sine wave. This is a symptom of a louder sound wave having a greater amplitude. If we reduced the amplitude of the sound wave to 40 dB or less, then the sine wave would begin flattening.

Now, let's say we're interested in playing a different note on the keyboard, such as C5. The C5 key produces a sound at 523 Hz, which creates a sound wave with more crests and troughs. Actually, each key is associated with its own frequency. As we move up the keyboard, the frequency of each key increases. For this example, we'll assume the key has an amplitude of 60 dB, similar to the most recent sound wave. As a result, the sound wave produced by hitting the C5 key could look like the following sine wave:

Again, frequency translates over to pitch. In other words, the faster a wave repeats itself, the higher the pitch of the sound produced by hitting a key. Meaning, hitting the C4 key will cause its string to vibrate at 523 Hz, whereas hitting the C5 key will cause its string to vibrate at 523 Hz. To be clear, this is true for all instruments, and isn't only true for pianos. If a vocalist sings a C4 note, then the vocalist's throat will vibrate at 262 Hz.

In most cases throughout the world, sounds aren't perfect sine waves. Sounds are usually layered on top of each other, consisting of varying amplitudes and frequencies. In the next section, we'll illustrate layered sounds and how they can be interpreted.

Additive Synthesis

Additive synthesis is a technique involving many simple tones being added together to make a more complex tone. This concept arises from an idea mentioned earlier: complex sounds are made up of simpler sounds. In additive synthesis, this concept is applied in reverse.

Interestingly, additive synthesis has been used by instruments to produce sounds since the Middle Ages. Specifically, the pipe organ uses a separate pipe for each tone being added, which produces a resulting complex sound. As the performance of computers continues to improve, digital software has become a popular means for mixing more complex sounds. As a result, complex sounds become limited by the performance of the computer, rather than the number of pipes in a physical instrument, such as the pipe organ. In othe words, digital oscillators and other modern systems can mix thousands of sine waves in real time, using aditive synthesis. In more recent software, additive synthesis has been replaced by more efficient techniques used for producing complex sounds.

In theory, any waveform can be added together in order to form a more complex sound. However, sine waves are the most popular waveform that is used, since it's considered the purest waveform. In other words, a sine wave doesn't consist of any harmonics, which is an additional wave that's layered on top of a fundamental wave, where the frequency of the layered wave is an integer multiple of the frequency of the fundamental wave.

By using sine waves when performing additive synthesis, the process becomes simpler, controllable, and predictable. Additive synthesis can be used to create other common waveforms, such as square and saw waves. These waves are interesting because their harmonics follow a well-structured pattern. For example, an ideal square wave consists of odd-integer harmonic frequencies.

To help visualize some of these concepts, we'll depict the addition of two sine waves. In particular, one sine wave has an amplitude of 40 dB and a frequency of 294 Hz, while the other sine wave has an amplitude of 40 dB and a frequency of 523 Hz. This is similar to playing the C4 and C5 notes on a keyboard at the same time. The following visual illustrates the resulting sound wave:

Notice, the above sound wave doesn't emulate the typical shape of a sine wave. The shape of this sound wave is the result of additive synthesis, which roughly represents the two basic sine waves layered on top of each other. In other words, the two sine waves are added together to create the more complex sound wave seen above.

A more concrete application of additive synthesis can be found when playing a chord on the keyboard. In this scenario, let's say our chord includes exactly 3 notes. As a result, the outcome becomes a sound wave representing the three individual sound waves added up together.

Next Steps

This post was heavily influenced by this amazing article. In the future, I plan to include details about harmonics and addtional waves, such as square and saw waves. Specifically, I hope to illustrate some of these more complex concepts with waveforms and other graphics. Also, I want to describe the differences between sine waves and other waveforms.