Inception

Motivating $1 \times 1$ Convolutions

• A modest number of $5 \times 5$ convolutions can be expensive if the number of filters is large
• Therefore, we would like to apply dimensionality reduction when the computational requirements increase too much
• A $1 \times 1$ convolution is used to compute reductions before the expensive $3 \times 3$ nad $5 \times 5$ convolutions
• Besides being used as dimensional reductions, they also include the use of relu activation functions

• In other words, these convolutional layers transform our input such that:

  • $J$ decreases to some degree
  • The dimensions (of the output) are reduced
• For these reasons, this concept is sometimes referred to as a network in network

Interpreting $1 \times 1$ Convolutions

• A $1 \times 1$ convolution refers to an image convolved with a $1 \times 1$ filter

• This convolutional layer can be thought of as a fully-connected layer such that:

  • The image's pixels represent the previous layer's activations
  • A single filter represents a single neuron within a hidden layer
• Here, each pixel represents a neuron
• Remember, each value from a filter represents a weight
• Adding additional filters to a convolutional layer is similar to adding additional neurons to the hidden filter

Illustrating Network in Network

• As we go deeper in a network, sometimes the number of channels grows too much
• We may want to reduce add a convolutional layer that reduces the number of channels without reducing the height and width of our image

• Specifically, we may want to have a filter that transforms our image such that:

  • $n_{h}$ and $n_{w}$ remain the same
  • $n_{c}$ decreases
• In this case, we would want to convolve an image with a $1 \times 1$ filter

Motivating the Inception Network

• When designing a layer for a convolution network, we'll need to choose which filter to use

• Inception networks take into account two questions:

  • Should we use a $3 \times 3$ filter, a $1 \times 3$ filter, a $5 \times 5$ filter, etc?
  • Should we use a convolutional layer or a pooling layer?
• In other words, we'll need to find the set of hyperparameters for a filter that minimizes the cost $J$
• The inception network essentially tries all of them
• This makes the network more complicated, but significantly increases the accuracy

Describing the Inception Network

• Instead of choosing a single filter size, we could try them all
• In this case, we need to adjust the padding to ensure the resultant images are the same size
• Then, our optimization algorithm will determine the weights
• Meaning, our optimization algorithm decides which filters to use
• For example, we can try different convolutional filters and max-pooling filters
• Each resultant volume is then stacked on top of each other
• We may ask ourselves how to choose the number of filters associated with a distinct filter
• Roughly, we can interpret the number of distinct filters as the number of chances for the specific filter to detect different features in an image
• There is no hard rule, so this hyperparameter should be tuned
• Generally, if this hyperparameter is too small, then we could possibly lose information by overfitting a particular filter
• On the other hand, if this hyperparameter is too large, then we could also lose information by underfitting a particular filter

Handling the Computational Cost

• Computing the inception layer from above would lead to $120$ million multiplications
• Although we can compute this amount of computations, it becomes very expensive
• Instead, we can include a $1 \times 1$ convolutional layer before the large inception layer
• This $1 \times 1$ convolutional layer is called a bottleneck layer
• Including a bottleneck layer will reduce the dimensionality of the input image
• As a result, computing the inception layer would lead to only $12.4$ million multiplications

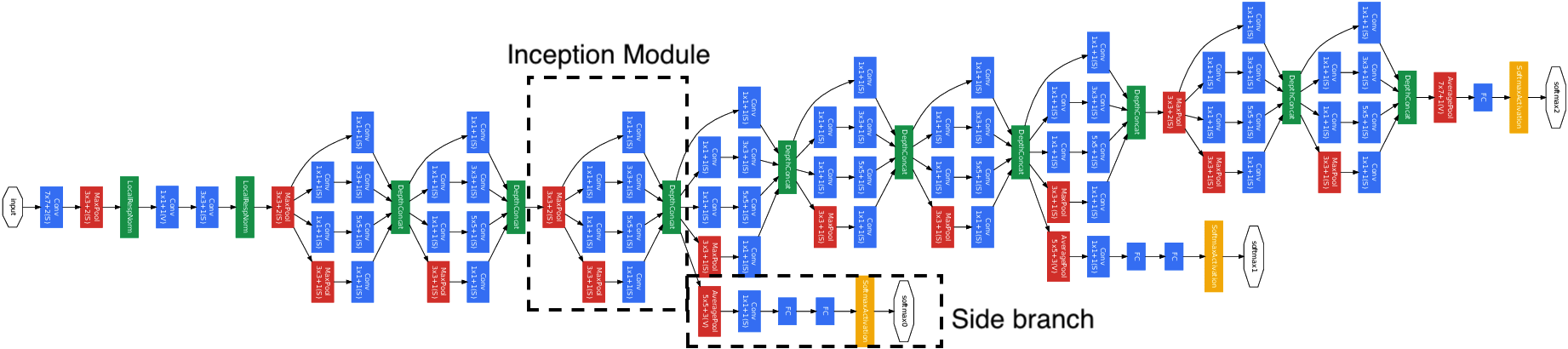
Inception Network

• An inception network contains many repeated inception modules
• These inception modules are generally made up of layers containing the same convolutional and max-pooling filters
• An inception network also contains side branches
• These side branches are made up of convolutional layers that lead into a softmax layer
• These side branches are located throughout our network branched from a few hidden layers
• These side branches make predictions to help prevent overfitting
• Specifically, this has a regularization effect on the network

---

tldr

• $1 \times 1$ convolutional layers transform our input such that:

  • $J$ decreases to some degree
  • The dimensions (of the output) are reduced

• These convolutional layer can be thought of as a fully-connected layer such that:

  • The image's pixels represent the previous layer's activations
  • A single filter represents a single neuron within a hidden layer
• Adding additional filters to a convolutional layer is similar to adding additional neurons to the hidden filter
• An inception layer essentially tries a bunch of convolutional and max-pooling filters to find the most effective ones
• This makes the network more complicated, but significantly increases the accuracy
• An inception network contains many repeated inception modules and side branches

---

References

• Inception Network Motivation
• Definition of an Inception Network
• Definition of a Network in Network
• Inception Paper
• Intuition of 1x1 Convolution
• How Depth is Determined