Reformers

Motivating Tasks with Long Sequences

• Transformers work well on fairly long sequences
• However, if sequences grow extremely long, the transformer must be tweaked to receive the necessary performance improvements

• There are a growing number of NLP tasks requiring longer sequences:

  • Writing books
  • Storytelling
  • Building chatbots

• The transformer models behind these tasks become slow for training

  • Due to the increased size of inputs
  • Thus, slowing the training of these very long sequences

• Many are based on the GPT-3 transformer model

  • This is just a larger version of GPT-2

• Unfortunately, training these models can require:

  • Industrial compute resources
  • Industrial cost

• Processing long text sequences is at the core of building chatbots

  • A chatbot must use every previous piece of the conversation as inputs for the next reply
  • This leads to very large context windows

How Chatbots Differ from Question and Answering

• Recall, contextual question and answering models require both a question and a relevant answer during testing and evaluation

• Whereas, closed-loop question and answering models don't require a relevant answer during testing and evaluation

  • The relevant answers have already been learned during training
  • All the knowledge is stored in the weights of the model itself during training
• This is how a chatbot functions

Describing the Complexity of a Transformer

• Training transformers on larger sequences becomes slow

  • The number of parameters required for an accurate enough model grows to be a very large number
  • Consequently, modern GPUs will run out of memory when trying to load all of these parameters

• The two primary causes of this memory inefficiency are:

  • Increasingly longer input sequences

    • Mathematically, this correlates with more attention computations

  • Larger hidden layers

    • Mathematically, this correlates with more saved

• Calculating attention scores on an input and output sequence of length $L$ takes $L^{2}$ time and memory

  • Suppose $L=100$

    • $L^{2}=10,000$
    • Then $10$ operations is computed per $1$ second

  • Suppose $L=10,000$

    • $L^{2}=10,000,000$
    • Then $1$ operation is computed per $10$ seconds
  • Modern GPUs perform around $10,000,000$ operations per second

• Having $N$ layers of attention takes $N$ times as much memory

  • GPT-3 already has $96$ layers
  • Even modern GPUs can struggle with this kind of dimensionality

• Recall, an attention score is the $\text{softmax}(Q \times K^{T}) \times V$

  • Where $Q$ is a query
  • Where $K$ is a key
  • Where $V$ is a value

• $Q$, $K$ and $V$ are all of dimension $L \times d_{model}$

  • Where $L$ is the length of a sequence
  • Where $d_{model}$ is the depth of attention
• Thus, $Q \times K^{T}$ will $L^{2}$ in length

Summarizing the Problems Causing Transformer Complexity

• Again, the two primary causes of memory inefficiency are:

  • Longer sequences leading to more attention computations
  • Larger hidden layers leading to more saved forward-pass activations used in backward propagation

• LHS attention layers solve our first problem

  • Keep in mind, when handling long sequences, we usually don't need to consider all $L$ positions
  • Instead, we can just focus on an area of interest instead

  • For example, suppose we're translating long English text to German

    • We don't need to consider every English word at once

    • Instead, we can use attention and focus on the following:

      • A single English word being translated
      • Those words immediately around that English word

• Reversible residual layers solve our second problem

  • Generally, the more layers a model has, the more memory it needs
  • Since, we must store the forward pass activations for backprop
  • We can overcome this memory requirement by recomputing activations
  • However, it needs to be done efficiently to minimize taking too much extra time

  • For example, GPT-3 would take a very long time to recompute activations

    • Thus, we need a way to speed up this re-computation, such that it's efficient to use less memory

Motivating LHS Attention

• To motivate LHS attention, we'll map words to other potentially relative words based on its attention scores

• Notice, the attention scores of it only focuses on certain words

  • On the left panel, it refers to animal instead of street
  • On the right panel, it refers to street instead of animal

• For both sentences, there are only a few relevant attention scores

  • Specifically, we're only really interested in the nouns

• Thus, we only should be interested in keeping the relevant attention scores for each word

  • To do this, we can use KNN with locality sensitive hashing

Illustrating LSH Attention

• We can use locality sensitive hashing (LSH) to reduce the computational costs of finding $K$ nearest neighbors

  • The same approach can be applied for computing attention

• Using LSH, we can hash both the query $q$ and key $k$

  • This helps group similar query and key vectors together
  • In other words, this helps us group nouns with pronouns
• Then, we'll only need to run attention on keys that are in the same hash buckets as the query
• When choosing the hash, the bucket roughly must be the same sizes

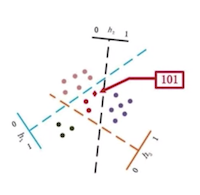
• Here, the hash of x equals the following:

  $$\text{hash}(x) = \text{sign}(x \times R)$$
  • $R$ is a random coefficient
  • The size of $R$ is $d$ for dimension $\times$ the number of hash bins
  • The $\text{sign}$ value determines the side of the plane the hash lands on
• This process is repeated for each hash value

• LSH is a probabilistic, not a deterministic model

  • This is because of the inherent randomness $R$ within the LSH algorithm
  • Meaning, that the hash can change along with the buckets a vector finds itself mapped to

Defining the Steps of LSH Attention

• These are the LSH steps applied to attention scores:

  1. Modify the model so it outputs a single vector at each position

     • Each vector is mapped to the relationship between a $q$ and $k$
     • This is referred to as $QK$ attention
  2. Hash $Q$ and $K$ to map each vector to a bucket with LSH
  3. Sort the vectors by LSH bucket

  4. Perform standard attention $\text{softmax}(QK^{T})V$ within the same hash bins (LSH buckets)

     • This reduces the search space for each $K$ to the same LSH bucket as $Q$

     • Take advantage of hardware parallelism by performing batch computation

       1. Split the sorted sequence into fixed size chunks

          • This allows for some parallel computation

       2. Let each chunk attend within itself and the adjacent chunks

          • This covers the case of a hash bucket that is split over more than one chunk

            • E.g. the blue, yellow, and magenta buckets

Introducing a Reversible Residual Layer

• Suppose we're interested in learning the text of an entire book
• We could input the tokenized words into a transformer
• Meaning, possibly $1$ million tokenized words would be processed
• Each token has an associated feature vector of some size

• Meaning, just the input for the model could be $2\text{GB}$ in size

  • On a $16\text{GB}$ GPU, this is $\frac{1}{8}$ of the total memory budget
  • Notice, we haven't even touched the layers yet
• The size of the inputs and outputs for each layer will also be $2\text{GB}$

• To do backpropagation through this model, the forward path will need to store some intermediate quantities in memory

  • These are the forward-pass activations for each layer

• Saving these activations would use around $50\text{GB}$ of memory

  • This won't fit on a single device
• Keep in mind, the latest transformers are much deeper than $12$ layers
• Fortunately, reversible residual layers can mitigate this problem
• To do this, they efficiently save activations for the backward path

Defining a Reversible Residual Layer

• This transformer repeatedly adds residuals to the hidden states

  • There are only two hidden states used in transformers:

    • Feed forward layers
    • Attention layes

• To run it in reverse, you can subtract the residuals in the opposite order

  • Starting with the outputs of the model

• In order to save memory used to store the residuals, we must recompute them quickly

  • This is where reversible a residual layer (RRL) comes in

• The general process of RRL is the following:

  1. An RRC must start with two copies of the model inputs

     • This enables reversible residual blocks
  2. Each layer only computes one of the copies

  3. The activations unused in updates will be used to compute the residuals

     • Now, we can run the network in reverse

• The activations in the model are now twice as big

  • However, we don't need to cache for the backwards pass now
• The standard transformer represents the normal residual connections

• The standard transformer uses the following formulas:

  • Attention Layer: $y_{a} = x + \text{attention}(x)$
  • Feed-forward Layer: $y_{b} = y_{a} + \text{feedforward}(y_{a})$

• The RRL uses the following formulas:

  • Attention Layer: $y_{1} = x_{1} + \text{attention}(x_{2})$
  • Feed-forward Layer: $y_{2} = x_{2} + \text{feedforward}(y_{1})$
• To save memory, we reconstruct the inputs $x_{1}$ and $x_{2}$:

$$x_{1} = y_{1} - \text{attention}(x_{2}) \\ x_{2} = y_{2} - \text{feedforward}(y_{1})$$

• Essentially, we're computing using one side of the network plus feedforward of the other side to compute $y_{2}$
• Similarly, one side of the network $+$ attention of the other side to compute $y_{1}$
• By doing this, we can recompute $x_{1}$ and $x_{2}$ efficiently

Defining a Reformer Model

• Week 4: Video: Reformers

References

• Stanford Deep Learning Lectures
• Stanford Lecture about LSTMs
• Lecture about the Complexity of Transformers
• Lecture about LHS Attention
• Lecture about Reversible Residual Layers
• Lecture about the Reformer Model
• Paper about the Efficient Reformer Model
• Google AI Article about Attention Scores
• Paper about Alignment and Attention Models
• Post about Attention with Recurrent Neural Networks