Face Recognition

Differentiating between Face Verification and Recognition

• Face verification

  • We input an image and a name ID
  • A face verification method outputs if the image belongs to that claimed name ID
  • Face verification is typically easier than face recognition
  • This is because we only need to verify a single face to one ID
  • Specifically, the accuracy needs to be around $99$

• Face recognition

  • We input an image
  • A face recognition method outputs if the image belongs to any name IDs
  • Face recognition is typically harder than face verification
  • This is because we need to verify a single face to many IDs
  • Specifically, the accuracy needs to be around $99.99$

Motivating One-Shot Learning

• Typically, we'll only have a single image associated with a name ID in our database
• Most face recognition systems need to learn from this one image
• Consequently, the learning algorithm trains on a small sample
• This problem is called the one-shot learning problem
• The one-shot learning problem is one of the main challenges for most face recognition systems

Describing One-Shot Learning

• Instead of learning the weights from a convolutional network, we want to learn a similarity function
• This similarity function measures the difference between two images
• Specifically, the similarity function is defined as the following:

$$d(x_{1}, x_{2}) = \Vert f(x_{1}) - f(x_{2}) \Vert_{2}^{2}$$

• Where $x_{1}$ and $x_{2}$ are two different images

• Where $f(x_{1})$ and $f(x_{2})$ are the activations of a fully-connected output layer from a siamese network

  • We will talk about the siamese network in the next section

• The similarity function returns:

  • A small number if the two images are similar
  • A large number if the two images are different
• This is defined as the following:

$$d(img_{1}, img_{2}) \le \tau \implies \text{similar}$$ $$d(img_{1}, img_{2}) > \tau \implies \text{different}$$

• Here, $\tau$ represents some threshold hyperparameter
• This is the root of all face verification problems
• For face recognition, we would need to calculate this similarity function on the input image and each image in our database

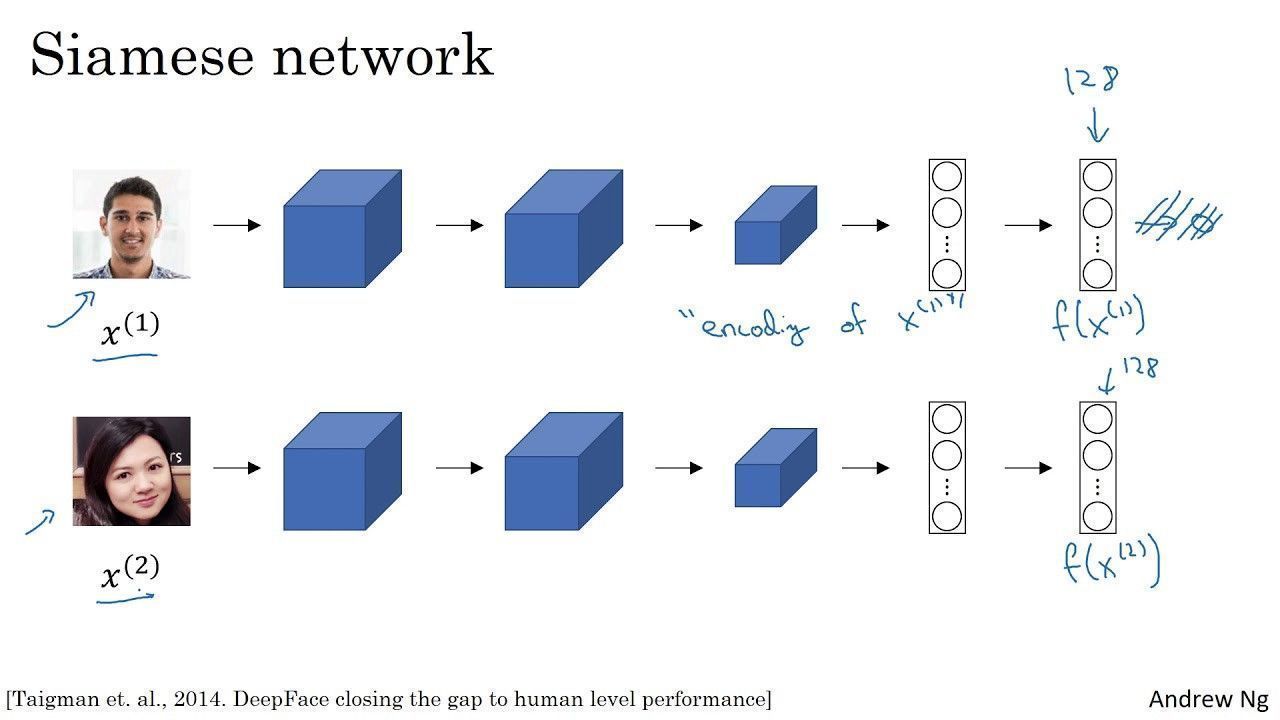
Introducing Siamese Network

• A siamese network is a convolutional network found in face recognition problems
• Roughly, a siamese network encodes an input image into a $128$-digit vector
• Specifically, a siamese network architecture refers to running two different images on an identical network
• A siamese network is trained such that the similarity function ensures encodings (or output layer) of the same person return a small value

• In other words, a siamese network learns parameters such that:

  • If $x_{i}$ and $x_{j}$ are the same person, then $\Vert f(x_{i}) - f(x_{j}) \Vert_{2}^{2}$ is small
  • If $x_{i}$ and $x_{j}$ are different people, then $\Vert f(x_{i}) - f(x_{j}) \Vert_{2}^{2}$ is large
• Formally, parameters of a siamese network define an encoding $f(x_{i})$
• Formally, an input image $x_{i}$ will be encoded into a $128$-digit vector $f(x_{i})$

Defining the Triplet Loss Function

• A siamese network uses a triplet loss function
• The triplet loss function is defined as the following:

$$tp = \Vert f(x^{a}) - f(x^{p}) \Vert_{2}^{2} - \Vert f(x^{a}) - f(x^{n}) \Vert_{2}^{2} + \alpha$$ $$\mathcal{L}(x^{a}, x^{p}, x^{n}) = \max(tp, 0)$$

• Here, $f(x^{a})$ refers to the encoded activations of an anchor image
• Here, $f(x^{p})$ refers to the encoded activations of a positive image
• Here, $f(x^{a})$ refers to the encoded activations of a negative image
• An anchor image refers to an input image we want to test
• A positive image refers to a saved image that is the same person from the anchor image
• A negative image refers to a saved image that is not the same person from the anchor image

Describing the Triplet Loss Function

• The term triplet loss comes from always needing to train on three images at a time
• Therefore, we will need multiple pictures of the same person
• For example, we may need $10$ pictures for each person
• We want the encodings of the anchor image to be very similar to the positive image and very different from the negative image
• Formally, we want the following:

$$\Vert f(x_{i}^{a}) - f(x_{i}^{p}) \Vert_{2}^{2} \quad \le \quad \Vert f(x_{i}^{a}) - f(x_{i}^{n}) \Vert_{2}^{2}$$

• This can also be written as the following:

$$\Vert f(x_{i}^{a}) - f(x_{i}^{p}) \Vert_{2}^{2} - \Vert f(x_{i}^{a}) - f(x_{i}^{n}) \Vert_{2}^{2} \quad \le \quad 0$$

• We can satisfy this equation by setting each term to $0$:

$$\Vert \underbrace{f(x_{i}^{a}) - f(x_{i}^{p})}_{0} \Vert_{2}^{2} - \Vert \underbrace{f(x_{i}^{a}) - f(x_{i}^{n})}_{0} \Vert_{2}^{2} \quad \le \quad 0$$

• Obviously, we don't want our network to train our images such that our encodings become equal to $0$
• Meaning, the encoding would be equal to the encoding of every other image
• Therefore, we need to modify the objective such that our terms are smaller than $0$:

$$\Vert f(x_{i}^{a}) - f(x_{i}^{p}) \Vert_{2}^{2} - \Vert f(x_{i}^{a}) - f(x_{i}^{n}) \Vert_{2}^{2} \quad \le \quad 0 - \alpha$$

• We need to tune the hyperparameter $\alpha$ to find the right threshold
• The hyperparameter $\alpha$ is referred to as a margin
• Including $\alpha$ will prevent our network from learning those trivial solutions
• We can reformulate the formula to be the following:

$$\Vert f(x_{i}^{a}) - f(x_{i}^{p}) \Vert_{2}^{2} - \Vert f(x_{i}^{a}) - f(x_{i}^{n}) \Vert_{2}^{2} + \alpha \quad \le \quad 0$$

Example of the Triplet Loss Function

• Let's say we set $\alpha=0.2$
• Then, our output could be the following:

$$\Vert f(x_{i}^{a}) - f(x_{i}^{p}) \Vert_{2}^{2} + \underbrace{\alpha}_{0.2} = 0.5$$ $$\Vert f(x_{i}^{a}) - f(x_{i}^{n}) \Vert_{2}^{2} = 0.51$$ $$\underbrace{\Vert f(x_{i}^{a}) - f(x_{i}^{p}) \Vert_{2}^{2} + \alpha}_{0.5} \quad \le \quad \underbrace{\Vert f(x_{i}^{a}) - f(x_{i}^{n}) \Vert_{2}^{2}}_{0.51}$$

• We can see that these terms satisfy our triplet loss condition
• Obviously, we would prefer for the gap to be larger between our positive and negative images
• For example, we'd prefer the following at the very least:

$$\underbrace{\Vert f(x_{i}^{a}) - f(x_{i}^{p}) \Vert_{2}^{2} + \alpha}_{0.5} \quad \le \quad \underbrace{\Vert f(x_{i}^{a}) - f(x_{i}^{n}) \Vert_{2}^{2}}_{0.7}$$

• Alternatively, we could push the $d(a,n)$ up or $d(a,p)$ down
• However, we'd obviously prefer to satisfy both conditions

Choosing the Triplets $x^{a}$, $x^{p}$, and $x^{n}$

• We don't want to randomly choose $x^{a}$, $x^{p}$, and $x^{n}$
• If we randomly choose these images, then $d(x^{a}, x^{p}) + \alpha \le d(x^{a}, x^{n})$ is easily satisfied
• Therefore, we'll want to choose triplets that are hard to train on when construction our training set
• Meaning, we want to choose $x^{a}$, $x^{p}$, and $x^{n}$ so that this is initially true early on in training:

$$d(x^{a}, x^{p}) \approx d(x^{a}, x^{n})$$

---

tldr

• One-shot learning is a training algorithm
• Specifically, one-shot learning involves training on two images such that the similarity between the two images is minimized
• This similarity function is defined as the following:

$$d(x_{1}, x_{2}) = \Vert f(x_{1}) - f(x_{2}) \Vert_{2}^{2}$$

• A siamese network is a convolutional network found in face recognition problems
• Roughly, a siamese network encodes an input image into a $128$-digit vector

• A siamese network learns parameters such that:

  • If $x_{i}$ and $x_{j}$ are the same person, then $\Vert f(x_{i}) - f(x_{j}) \Vert_{2}^{2}$ is small
  • If $x_{i}$ and $x_{j}$ are different people, then $\Vert f(x_{i}) - f(x_{j}) \Vert_{2}^{2}$ is large
• A siamese network uses a triplet loss function
• The triplet loss function is defined as the following:

$$tp = \Vert f(x^{a}) - f(x^{p}) \Vert_{2}^{2} - \Vert f(x^{a}) - f(x^{n}) \Vert_{2}^{2} + \alpha$$ $$\mathcal{L}(x^{a}, x^{p}, x^{n}) = \max(tp, 0)$$

• The term triplet loss comes from always needing to train on three images at a time
• Therefore, we will need multiple pictures of the same person
• We want the encodings of the anchor image to be very similar to the positive image and very different from the negative image
• We want to choose triplets that are hard to train on when construction our training set

---

References

• Difference between Face Recognition and Verification
• One-Shot Learning
• Siamese Network
• Triplet Loss Function