Face Verification

Differentiating between Face Verification and Recognition

• Face verification

  • We input an image and a name ID
  • A face verification method outputs if the image belongs to that claimed name ID
  • Face verification is typically easier than face recognition
  • This is because we only need to verify a single face to one ID
  • Specifically, the accuracy needs to be around $99$

• Face recognition

  • We input an image
  • A face recognition method outputs if the image belongs to any name IDs
  • Face recognition is typically harder than face verification
  • This is because we need to verify a single face to many IDs
  • Specifically, the accuracy needs to be around $99.99$

Describing Face Verification

• The training process of a face verification network is very similar to the training process of a face recognition network
• Specifically, we would still train a siamese network
• However, we add an extra layer after the $f(x)$ embeddings

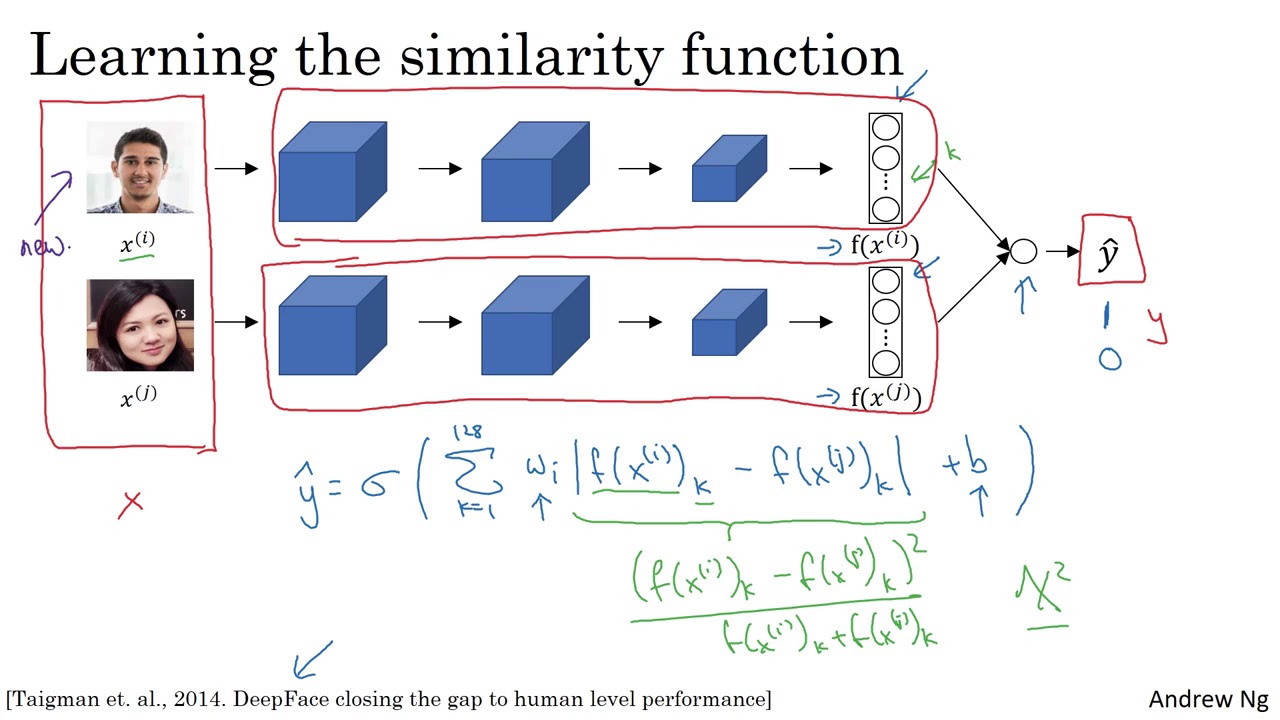
• This extra layer contains a single sigmoid neuron

• Specifically, this output layer outputs:

  • A $1$ if the two images are the same
  • A $0$ if the two images are different
• Therefore, we are not using a triplet loss anymore
• Instead, we are using a cross-entropy loss function

Defining the Network

• The output of our network becomes a sigmoid function applied to the features
• These features aren't only the embeddings
• Instead, the activations $a^{[l-1]}$ become the following:

$$\vert f_{k}(x^{(i)}) - f_{k}(x^{(j)}) \vert$$

• Here, $k$ represents the $k^{th}$ component of the $128$-digit vector
• Then, the output of our network becomes the following:

$$\hat{y} = \sigma(\sum_{k=1}^{128} w_{i}^{[l]} a^{[l-1]} + b^{[l]})$$ $$\hat{y} = \sigma(\sum_{k=1}^{128} w_{i} \vert f_{k}(x^{(i)}) - f_{k}(x^{(j)}) \vert + b)$$

• We can use other variations of the $a^{[l-1]}$ term
• For example, we could use the $\chi^{2}$ similarity:

$$\chi^{2} = \frac{(f_{k}(x^{(i)}) - f_{k}(x^{(j)}))^{2}}{f_{k}(x^{(i)}) - f_{k}(x^{(j)})}$$

• There are many other variations of possible similarity functions
• Instead of training triplets, we are only training pairs of images

---

tldr

• The training process of a face verification network is very similar to the training process of a face recognition network
• Specifically, we would still train a siamese network
• However, we add an extra layer after the $f(x)$ embeddings
• This extra layer contains a single sigmoid neuron
• The output of our network becomes a sigmoid function applied to the features
• These features aren't only the embeddings
• Instead, the activations $a^{[l-1]}$ become the following:

$$\vert f_{k}(x^{(i)}) - f_{k}(x^{(j)}) \vert$$

• Instead of training triplets, we are only training pairs of images

---

References

• Face Verification